There’s an Easier Way for Children to Learn Multiplication!
For years, I have watched children struggle with Multiple-Digit Multiplication, which begins with problems like, 97 x 86, then quickly increases in difficulty to problems like, 5,984 x 763, and finally culminates in multiplying decimals like 5.83 x 7.3. Memorizing all the multiplication facts can be difficult for some kids. Children who are struggling with Multiple-Digit Multiplication are smart kids! However, they have some gaps in their learning when it come to multiplication. Simply repeating the same strategies they were taught when they first started learning multiplication will not work.
I looked for an easier strategy – one where all children would be successful multiplying large numbers. I decided to incorporate Counting by the Numbers, an Area Box, and Simple Addition. I taught this strategy to my 6th graders who struggle with multiple-digit multiplication. After completing my series, every one of them were able to pass the educational standards for multiple-digit multiplication!
3-Steps Make Multiplication Simple!
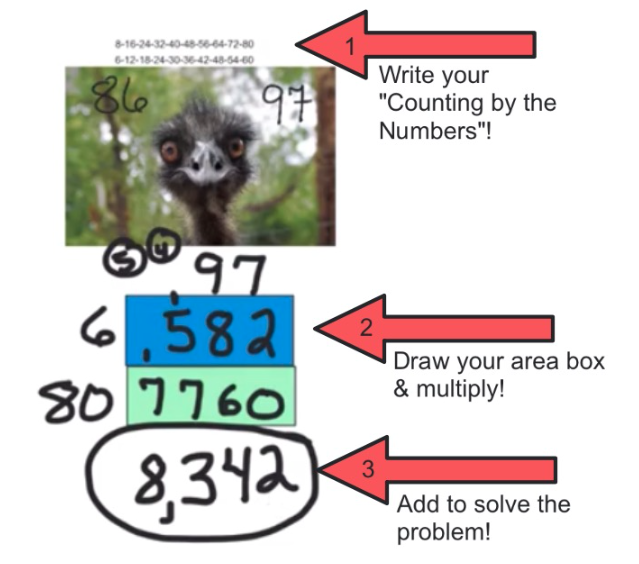
Step 1 – Write your “Counting by the Numbers” for one of the factors (the numbers you are multiplying). In this case I wrote 8’s and my 6’s.
Step 2 – Draw your Area Boxes. In this case I need two area boxes, one for the 6 and another for the 80. Next, Use the counting by the numbers to multiply these numbers. (I demonstrate this strategy in a video below).
Step 3 – Finally, add all your products together.
Area Multiplication
is
Designed so that
ANYONE can Succeed at Multiplication!
Hello, my name is Brian McCoy, and I am a credentialed teacher in the state of California. I have been teaching elementary and middle school children for over a quarter of a century. After years of watching children struggle with the algorithm for multiplying large numbers, I set out to develop an easier method. I created Area Multiplication.
Let me be clear, Area Multiplication is NOT for children who can already multiply large numbers like 574 x 763. The process does take a bit more time. However, Area Multiplication is structure in such a way that absolutely anyone can successfully multiply large numbers.
WHEN CHILDREN DO NOT KNOW THEIR MULTIPLICATION FACTS…
THEY NEED A STRATEGY!
By simply writing the “counting by the numbers” above their problem, children who do NOT know their multiplication facts can succeed! For example, with the problem 97 x 86; Children can write “counting by the numbers” for 8’s and the 6’s. The mathematical model at the top of this page shows the results.
My goal is for children is to memorize their multiplication facts. However, until they know all their facts, they need a strategy. Counting by the numbers is the easiest strategy to learn. Therefore, I have added “counting by the numbers” to the end of each video. Children who do not know all their multiplication facts should watch and count with me at the end of each of these videos until they can count by all the number on their own. Repetition of this strategy will help in all areas of math that require multiplication. Once a child knows all their multiplication facts, they can stop the videos after the problem is solved and before Counting by the Numbers begins.
This Math Help Website is Designed to build a concrete understanding of Multiplication!
All Problems have Math Video Tutorials!
Cyclical Learning Approach
I have incorporated a cyclical learning approach with math tutorial videos. Each educational concept is introduced, then reinforced, then revisited again and again – with each subsequent step rising to the next level of competency. There are 5-lessons that take children from the basics of multiplication to multiplying decimals by decimals.
I have scaffold these problems:
-
- The first problem is a Watch ME.
Students should read the problem and then click on the video to watch how the problem is solved.
Students should copy the entire problem into their notebook. - The second problem is a WORK WITH ME.
Students should read the problem then gather all their materials, so that they can do the problem with me.
Students should play the math tutorial video and pause it when told.
Finally, Students should copy the problem down on their own paper, and solve it with me.
When the math tutorial video is complete, students should review the problem with their teacher or parent. - All the following problems are ON YOUR OWN.
Students should solve the problems just as they did in the first two.
Once you they completed the problem, they should watch the math tutorial video.
Students should keep their paper with them while they watch the video.
If they made a mistake, they should pause the math tutorial video and fix their mistake.
That’s the fastest way to learn!
- The first problem is a Watch ME.
Mastering Area Multiplication with 86 x 97
Problem: Multiplication Roadblocks
Imagine your child sitting at the kitchen table, pencil in hand, staring hopelessly at a daunting multiplication problem like 86 x 97. Frustration builds as they struggle to remember multiple steps, only to end up with the wrong answer.
Many children face this scenario, often because traditional methods don’t provide the visual clarity they need. Without a clear breakdown of the process, mistakes pile up, leaving children feeling defeated.
Activate: Why Area Multiplication is the Solution
The Area Multiplication method is a game-changer. By breaking the problem into smaller, manageable sections, children can see exactly how numbers combine to create the final answer. This method improves:
- Accuracy by minimizing errors.
- Confidence by simplifying each step.
- Understanding by reinforcing place value concepts.
Solution: Step-by-Step Breakdown of 86 x 97
- Break Each Number into Place Values
- 86 = (80 + 6)
- 97 = (90 + 7)
- Create a Grid
- Draw a 2×2 grid. Label the rows and columns with each place value.
- Multiply Each Section
- (80 x 90) = 7,200
- (80 x 7) = 560
- (6 x 90) = 540
- (6 x 7) = 42
- Add the Products
- 7,200 + 560 + 540 + 42 = 8,342
✅ The following are three samples from Book 1 on Area Multiplication!
Ernie the Photo-Hungry Emu
Ernie the Emu loves having his photo taken! As a matter of fact, Ernie gets his photo taken more than any other animal on the African Savanna. He sticks his face in front of anyone he sees with a smartphone or a camera . Ernie is 86 days old. He has had his photo taken 97 times every day of his life.
How many photos have been taken of Ernie the Photo-Hungry Emu?
Pinky Tuskadaro the Calculating Orangutan
Meet Pinky Tuskadaro the calculating orangutan! Right now, Pinky is trying to figure out how many bananas he has eaten in the past 48 days. If he ate 39 bananas each day,
How many bananas has Pinky eaten?
❌ Wrong Way John the Wandering Giraffe
Wrong Way John is a wandering giraffe who always gets stuck in the brambles! He traveled 36 miles a day for the past 27 days and got stuck 113 times.
How far did Wrong Way John travel in the past 27 days?
To Access this book in it entirety, Visit The Teacher’s Dungeon. All my books are free with you membership.
Real-World Case Study: Jessica’s Breakthrough
Jessica, a 4th grader, had struggled with multiplication for months. After using the Area Multiplication method, her accuracy improved dramatically. Within just two weeks, her test scores increased by 27%, and her math confidence soared. Jessica’s parents credit the method’s visual structure for helping her understand complex multiplication problems.
Conquering Larger Numbers with Area Multiplication: 94 x 368
Problem: Large Number Overwhelm
As numbers grow, so does the complexity of the multiplication process. Without a clear strategy, children often make careless mistakes or lose track of steps.
Activate: Why the Area Multiplication Method Works
The Area Multiplication method excels with larger numbers because it:
- Visually organizes each step.
- Minimizes confusion by isolating smaller calculations.
- Reinforces place value through clear sectioning.
Solution: Step-by-Step Breakdown of 94 x 368
- Break each number into place values:
- 94 = (90 + 4)
- 368 = (300 + 60 + 8)
- Draw a 2×3 grid and label each row and column.
- Multiply each section and add the products:
- (90 x 300) = 27,000
- (90 x 60) = 5,400
- (90 x 8) = 720
- (4 x 300) = 1,200
- (4 x 60) = 240
- (4 x 8) = 32
- Add all six results: 34,592
✅ The following are three samples from Book 2 on Area Multiplication!
Olivia Ostrich gets riled easily. As a matter of fact, Olivia screeches, flaps her wings, and stomps her feet every time she does not get her way. Some people say that she acts like a 3-year-old having a temper tantrum. Last year, Olivia had 63 temper tantrums each and every day.
How many temper tantrums did Olivia have in the past 365 days?
Meet Cameel & Kamel the Singing Camels. They are a brother-and-sister team that travel all over the world singing their beautiful melodies. They sing 74 songs at each concert. Cameel and Kamel are scheduled to perform 456 concerts.
How many songs will they sing?
Stone Cold Kelly is a killer. You can’t blame her—after all, she is an alligator , and alligators have to eat. However, Stone Cold Kelly only eats shrimp. She loves the taste of shrimp so much that she eats 85 shrimp at each meal.
How many shrimp will Stone Cold Kelly eat during her next 547 meals?
➡️ Want more math strategies like this? Each video tutorial is part of a comprehensive math book included with your TeachersDungeon membership. Visit TeachersDungeon.com to explore our full range of resources.
✅ The following are three samples from Book 3 on Area Multiplication!
Amos the Angry Kitten does not like ants. He just spotted one now, and he is ready to fight! On his daily prowl through the yard, Amos attacks an ant mound. There are 1,357 ants living there, and Amos fights every one of them.
If Amos battles each of the 1,357 ants every day for 46 days, how many ant-battles will Amos the Angry Kitten complete?
Montana the Lily-Loving Moose is always on the hunt for a tasty treat. He wades through the rivers looking for lily pads. Montana eats 3,492 lily pads each day. Yes, that is a lot of lily pads, but Montana is a BIG moose!
How many lily pads will Montana eat in the next 67 days?
Shelby & Sherman are a couple of thoroughbred seahorses. They are the two fastest seahorses in the entire world! Together, they have completed 38 races across the Pacific Ocean, from the Bering Strait to Antarctica’s Ross Sea, a total distance of 9,586 miles.
Altogether, how many miles have these two seahorses raced across the Pacific Ocean?
Joining The Teacher’s Dungeon gives you FREE access to a full collection of math books to support your child’s success.
✅ The following are three samples from Book 4 on Area Multiplication!
Hide and Go Seek Zeek is all about having fun! His favorite activity? Playing hide & seek. ♂️ Zeek plays for 9,463 seconds every day—that’s just under 3 hours! ⏳
If Zeek played every day for one year (365 days), how many seconds did he spend playing hide & seek?
Ignacio the Lettuce-Sharing Iguana is the friendliest iguana in all of Brazil! He always shares his lettuce with smaller iguanas. Over the past 749 days, Ignacio has shared 2,977 pieces of lettuce every single day.
How many pieces of lettuce did Ignacio share altogether?
Meet the Lazy Lion Pride! They nap more than any other pride of lions in the African Savanna. Each morning, this group of lions finds a comfortable branch and sleeps for exactly 9,876 seconds.
How many seconds will this pride of lions nap during the next 243 mornings?
Don’t miss out! All my math books are FREE with your membership to The Teacher’s Dungeon. Start exploring today!
✅ The following are three samples from Book 5 on Area Multiplication!
Stealthy Sea Otters live in a fishing port just north of San Francisco, California. They wait for the fishing boats to return with their catch, then they sneak in, all stealthy-like, and steal some of the fish. Yesterday, a boat came in with 0.607 tons of fish. The Stealthy Sea Otters stole 0.048 of the fish.
How many tons of fish did they steal?
Randy & Candy love to play! They are a couple of thoroughbred racehorses and are predicted to win The Kentucky Derby when they grow up. Last Tuesday, they spent 9.69 hours running, jumping, and frolicking through the pasture. A television news reporter filmed 0.037 of the time they were playing.
How many hours was Randy and Candy’s playtime on the news?
Pamela Panda the Singing Panda Bear can sing longer than any other bear in the world! Last year, at the National Bear Sing-Off, Pamela sang for 13 hours straight. This year, Pamela plans on singing 8.34 times longer. If Pamela accomplishes her goal, how long will she sing?
If Pamela accomplishes her goal, how long will she sing?
Want to see these books in there entirety? With your Teacher’s Dungeon membership, you’ll unlock FREE access to my entire collection of math books.
Don’t wait—join now!
