Top 10 Reasons Why Elementary Kids Need to Know About Negative Numbers

---

1️⃣ Real-Life Applications

Negative numbers appear in everyday life — from tracking temperatures ️ to checking bank balances . Understanding them early helps kids make sense of the world around them.

---

2️⃣ Foundation for Advanced Math

Negative numbers are essential in pre-algebra, algebra, and beyond. Learning them in elementary school builds a strong base for future success in middle and high school math.

---

3️⃣ Supports Number Sense

Understanding that numbers can exist below zero expands a child’s concept of the number system, reinforcing the idea that numbers are more than just “how many things.”

---

4️⃣ Improves Problem-Solving Skills

Working with negative numbers sharpens critical thinking and logic, especially when applied to subtraction, distance, and patterns.

---

5️⃣ Essential for Science Learning

Negative numbers are used in science concepts like elevation, temperature change, and electric charges, all of which are introduced early in STEM education.

---

6️⃣ Prepares for Real-World Math

Budgeting, measuring debt, or understanding sports scores (like goal differentials ⚽ or point spreads ) often involve negative numbers. It’s practical math!

---

7️⃣ Boosts Confidence with Math Language

Learning to interpret expressions like “greater than” or “less than zero” builds math vocabulary, helping students feel confident when speaking or writing about math.

---

8️⃣ Reinforces Opposites and Direction

Negative numbers help kids understand opposites (like up/down or gain/loss) and direction on a number line, which supports spatial reasoning and graphing.

---

9️⃣ Improves Understanding of Absolute Value

Once kids grasp negative numbers, they can better learn concepts like absolute value — a stepping stone to more advanced ideas like inequalities and distance.

---

Encourages Growth Mindset

Struggling to understand new ideas like negative numbers is part of building grit and resilience — critical life skills that transfer far beyond the math classroom.

The Hidden Struggles with Negative Numbers ➕➖

Imagine this: You’re checking your bank account, and instead of a positive balance, you see a big red -$50. What does that mean? It’s not just a number—it’s a concept that many students struggle to grasp. Negative numbers can feel like a math mystery ️‍♂️, and when inequalities, absolute value, and number line placement come into play, things get even trickier.

Parents and students alike often find themselves lost when tackling negative numbers, leading to frustration, confusion, and a lack of confidence in math. But don’t worry—we’re about to break it down in a way that makes complete sense! ✅

The Problem: Why Do Students Struggle with Negative Numbers?

Many students misunderstand negative numbers because they aren’t something we use regularly in our daily lives. Unlike counting apples or measuring distances , negative numbers represent things we owe, temperatures below zero, or elevations below sea level—abstract ideas that need concrete visuals to make sense.

Here are some key challenges students face:

• Misplacing negative numbers on a number line

• Reversing inequality signs when solving equations

• Not understanding the absolute value of a number
• Confusing subtraction with negative numbers ➖➖

Watch this video, How to Solve Negative Numbers when dealing with Absolute Values, for a deeper understanding of negative numbers.

The Aha Moment

Let’s step into the shoes of Emily, a 6th grader who once found negative numbers impossible. When asked to solve questions like the one below, she would freeze.

But then, something changed—her teacher introduced to the Teacher’s Dungeon, where every question is linked to a video tutorial.  The combination of fun questions, and immediate video tutorials helped – and suddenly, things started to click.

Here is a sample problem for the game:

Sandy the Side-Stepping Crab lives in Florida where the temperature is 92 degrees. She went on vacation in Alaska where the temperature is -46 degrees.
What was the difference in temperature?

Just like Emily, you can master negative numbers with the right tools.

Another strategy you can try at home is to introduced you child to a number line and real-world examples, Here’s how! ⬇️

The Solution: Four Key Strategies to Conquer Negative Numbers

1️⃣ Visualizing Negative Numbers with a Number Line ️

A number line is the best way to understand negatives. Picture a thermometer ️: above zero is positive, and below zero is negative.

Tip: When moving right, numbers get larger ➡️. When moving left, numbers get smaller ⬅️.

✅ Example: -5 is to the left of 0, and +5 is to the right.

Try this: Draw a number line and mark these values: -10, -5, 0, +5, +10. Now, practice adding and subtracting!

2️⃣ Solving Inequalities with Negative Numbers

Inequalities become tricky when negative numbers are involved because -8 is less than – 5! ⚠️. That is confusing for kids, because they are used to  positives, where 8 is greater than 5. 

✅ Example: If -8 < -5.

✏️ Draw a number line: 

 

Rule: Any number to the left of another is Less Than, and any number to the right of another is Greater Than!

3️⃣ Understanding Absolute Value as Distance

Absolute value is how far a number is from zero, no matter its direction. Think of it as a GPS measuring distance.

✅ Example: | -7 | = 7 because -7 is 7 spaces from 0.

✅ Example: | +7 | = 7 because +7 is also 7 spaces from 0.

Key Insight: Absolute value is always positive because it’s a measure of distance, not direction!

4️⃣ Finding the Difference Between Positive & Negative Numbers 

Understanding how to find the difference between positive and negative numbers is crucial. The key? Use a number line to give a concrete understanding of this abstract concept!

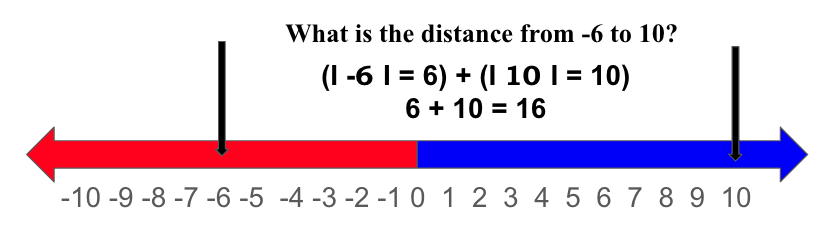
✅ First Example: What is the distance from -6 to 10?

Trick 1: Use the number line and count from -6 to 10 or from 10 to -6.

Trick 2: When you have one number in the negative and the other in the positive, use their absolute values and add them together.

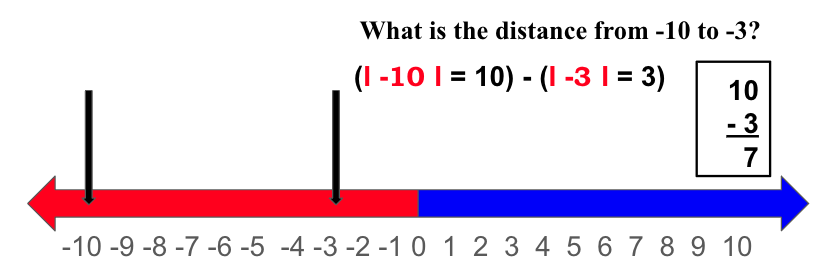
✅ Second Example: What is the distance from -10 to -3?

Trick 1: Use the number line to count from -10 to -3, or from -3 to -10.

Trick 2: When you have both number in the negative, use their absolute values – put the bigger number on the top and subtract them.

Real-World Application: Banking & Budgeting

Let’s go back to Emily. After mastering negative numbers, her teacher gave the class a pretend bank account.  Emily applied her skills to managing her money. At one point her teachers pretended to be the bank.  She loaned Emily $20, because she currently had $0 in her bank account.  That brought Emily’s bank balance to -$20.  Emily knew that she owed the bank $20. Later her teacher paid all of the students $50 for completing a science project.  Emily applied the math and discovered that she now had a positive $30 in her bank account.

Emily is rocking negative numbers — all thanks to understanding the number line and absolute values!

Lesson: Negative numbers aren’t just math problems—they’re real-life problem solvers!

Conclusion: You Can Master Negative Numbers!

Negative numbers don’t have to be confusing. With visual aids, simple rules, and real-world applications, students can go from struggling to confident problem-solvers.

Use a number line to visualize positive and negative numbers.

Think of absolute value as distance from zero—always positive.

Remember: When one number is in the negative and the other is in the positive, use their absolute values and add the numbers.

Remember: When both numbers are in the negative, use their absolute values – put the bigger number on the top and subtract.

 

With these strategies, negative numbers will no longer feel like a mystery.

Happy learning! ✨

Want More Math Hacks?

If you found this guide helpful, check out The Teacher’s Dungeon for interactive lessons, video tutorials, and personalized math support!

Sign up for a FREE trial today and take the frustration out of math!