Improper Fractions Are Confusing — Until You read This!
Let’s face it: Improper fractions are one of the most confusing concepts kids face in upper-elementary math.
- ❓ Why is ⁹⁄₄ more than a whole?
- ❓ Why does the numerator seem “too big”?
- ❓ How does any of this relate to real life?
Improper fractions trip up even confident students.
Questions like:
“Why is the top number bigger than the bottom?”
“Do I treat it like a whole number?”
“Why do I need to change it?”
…are all too common.
Many kids hit a wall with improper fractions, leading to math anxiety and falling behind in class. The reality? Improper fractions are a foundational skill—key to understanding everything from division to algebra.
If a child doesn’t grasp how to work with them, their confidence (and test scores) can quickly crumble.
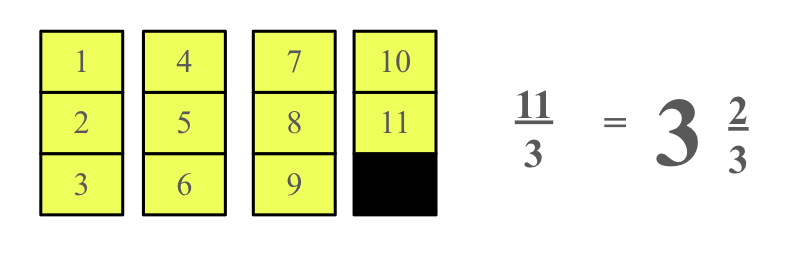
One of the best ways to help your child understand improper fractions is through visual learning. In the image above, you can see a visual representation of an improper fraction. These types of visuals are especially powerful for mastering concepts like converting mixed numbers, adding and subtracting improper fractions, and building a deeper understanding of how fractions work. Whether you’re supporting your child at home or looking for online math help for fractions, using models and real-world practice can make all the difference.
In this short but powerful article, I break down improper fractions in a way that finally makes sense — not just for kids, but for parents, too.
In the post, I’ll cover:
-
What an improper fraction really means (and why it’s not “wrong”)
-
How to visualize fractions greater than 1️⃣
-
Why converting to a mixed number helps us understand size and value
-
A clear, step-by-step example using real-world models
Watch the video to see an in-depth explanation of the photo above:
https://www.youtube.com/watch?v=TolQeG3Hfw0
⚡️Fractions Start Making Sense when we use math models!
Let’s look at Jasmine, a 6th grader who struggled with improper fractions. Her teacher moved fast through the material, and she was too afraid to ask questions. When her mom sat down to help, she realized Jasmine didn’t understand why improper fractions exist—only that they seemed “wrong.”
With the right visuals, real-life examples, and consistent practice (including a few videos from The Teacher’s Dungeon ), Jasmine not only caught up—she now helps her classmates!
The key? A step-by-step breakdown. That’s exactly what we’ll give you here.
How to Convert an Improper Fraction into a Mixed Number
Understanding improper fractions can be confusing for many students — especially when they first learn to convert them into mixed numbers. That’s why I have my students create math models like the one you saw in the video above. I teach a similar step-by-step and my students develop a concrete understanding of fractions and how they work..
The video above demonstrated how to turn an improper fraction (like 11/3) into a mixed number. With clear visuals, simple language, and real-time examples, your child will see how division and fractions work hand-in-hand.
Why math models matter:
-
Math Models build confidence with fractions
-
Math Models clearly show what is happening when you add, subtract, multiply, or division fractions
-
Math Models support 3rd through 6th grade Common Core Standards
Target Math Concept:
Converting an improper fraction into a mixed number by dividing the numerator by the denominator and identifying the whole number and remainder.
Real-Life Tip for Parents:
Many kids memorize the steps but don’t understand them. After watching the video above with your child and ask:
“Why do you think the remainder becomes the new numerator?”
That one question can unlock the concept in their mind!
Improper fractions are just fractions where the numerator is greater than or equal to the denominator. For example:
- 5/3 ✅ this equals 1 & 2/3
- 7/4 ✅ this equals 1 & 3/4
- 10/10 ✅ this equals 1
More Fraction Help
If your child is struggling with fractions — whether it’s adding, subtracting, multiplying, or dividing improper fractions — explore these full blog post:
Master Fractions: Multiplying & Dividing Fractions to Unlock Math Success for Your Child! ✨
Mastering Fractions: The Ultimate Guide to Adding and Subtraction Fractions with Unlike Denominators! ✨
Now let’s learn what to do with Improper Fractions. ✍️
➕ How to Add Improper Fractions
When adding improper fractions:
- Make sure denominators are the same.
- Add the numerators.
- Simplify if needed (or convert to a mixed number).
Example:
- 5/4 + 3/4 =
- (5+3)/4 =
- 8/4 = this also means 8 ÷ 4 =
- 2
Example:
- 7/6 + 5/6 =
- 12/6 = this also means 12 ÷ 6 =
- 2
Tip: Always reduce your answer or convert it to a mixed number if the problem asks!
➖ How to Subtract Improper Fractions
- Same denominator? Subtract numerators.
- Simplify if needed.
Example:
- 9/5 – 4/5 =
- (9-4)/5 =
- 5/5 = this also means 5 ÷ 5 =
- 1
Example:
- 11/6 – 3/6 =
- 8/6 = this also means 8 ÷ 6 =
- 1 & 2/6
- This can be simplified: 1 & 2/6 ÷ 2/2 = 1 & 1/3
Shortcut: Keep denominators the same before subtracting—don’t overcomplicate!
✖️ How to Multiply Improper Fractions
Multiply across numerators and denominators.
Example:
- (4/3) × (5/2) =
- (4×5)/(3×2) =
- 20/6 = this also means 20 ÷ 6 =
- 3 & 2/6
- This can be simplified: 3 & 2/6 ÷ 2/2 = 3 & 1/3
Example:
- 7/4) × (3/5) =
- 21/20 =
- 2 1/20 = this also means 21 ÷ 20 =
- 1 & 1/20
Always simplify the final answer!
➗ How to Divide Improper Fractions
Use the “Multiply the Reciprocal” rule:
- Keep the first fraction.
- Change the sign from ÷ to ×.
- Flip the second fraction.
- This is called “Multiply the Reciprocal“!
Example:
- (7/3) ÷ (2/5) =
- (7/3) × (5/2) = this is Multiplying the Reciprocal
- 35/6 = this also means 35 ÷ 6 =
- 5 & 5/6
Example:
- (9/4) ÷ (3/2) =
- (9/4) × (2/3) = this is Multiplying the Reciprocal
- 18/12 = this also means 18 ÷ 12 =
- 1 & 6/12
- This can be simplified: 1 & 6/12 ÷ 6/6 = 1 & 1/2
Pro Tip: This is where many students mess up—don’t forget to Multiply the Reciprocal!
Ever Wonder How to Divide a Whole Number by a Mixed Number? Watch the video below!
Dividing a whole number by a mixed number can feel like a math puzzle — even for adults! That’s why I created a video that breaks this tricky concept down in a way that’s clear, visual, and easy to follow for both students and parents.
In this short tutorial, you’ll learn:
-
How to convert the mixed number into an improper fraction
-
How to rewrite the whole number as a fraction over 1
-
How to multiply by the reciprocal
-
And most importantly — why these steps work
Why This Matters:
Mastering this skill is a key part of upper-elementary math (especially in 5th and 6th grade) and lays the foundation for more advanced concepts like ratios, algebra, and word problems involving fractions.
Real-Life Learning Tip for Parents
Many students memorize steps but struggle with why they’re doing them. After watching the video, ask your child:
“Can you explain why 1 & 1/2 turned into 3/2?”
If they can teach it, they truly understand it! ✨
In this video, we:
- Wrote the whole number as a fraction
- Converted the mixed number into an improper fraction
- Multiplied the Reciprocal to solve the problem!
- Created a Math Model to give a deeper understanding of the math!
Example in video:
- 3 ÷ 1 & 1/2 =
- 3/1 ÷ 3/2 =
- 3/1 × 2/3 = this is Multiplying the Reciprocal
- 6/3 = this also means 6 ÷ 3 =
- 2
Great for upper-elementary and middle school students!
BONUS Video: ➗ Dividing 1½ by 1¼ — Finally Made Simple!
Let’s be honest: Dividing mixed numbers like 1½ ÷ 1¼ can feel like math gymnastics — even for parents trying to help at home. But with the right strategy and visuals, this seemingly tricky concept becomes totally doable — and even fun!
In this quick video lesson, I walk you through how to divide 1 and ½ by 1 and ¼, step by step, using easy-to-understand Math Models and real math logic ✨.
https://www.youtube.com/watch?v=NDuVM915G-s
Let’s recap what’s Inside the Video:
-
How to convert both mixed numbers into improper fractions
-
The trick to “Multiply the Reciprocal”
-
Visual models that give a concrete understanding
-
A complete example using 1½ ÷ 1¼, explained clearly
-
How to simplify the answer and make it make sense
Example in video:
- 1 & 1/2 ÷ 1 & 1/4 =
- 3/2 ÷ 5/4 = convert into improper fractions
- 3/2 × 4/5 = Multiply the Reciprocal
- 12/10 = this also means 12 ÷ 10 =
- 1 & 2/10
- This can be simplified: 1 & 2/12 ÷ 2/2 =
- 1 & 1/5
What to make up your own Real World Applications?
Look at your recipes. Think of division problems like this: If you have 2 & 1/2 cups of flour and you want to make cookies where the recipe calls for 3/4 cup of flour. How many batches can you make?
- 2 & 1/2 divided into batches or groups of 3/4
- 2 & 1/2 ÷ 3/4 = ?
- Now it’s time to make up your own problems – Good Luck!
Final Thoughts: Fractions Don’t Have to Be Frustrating
Improper fractions feel intimidating because they look “wrong” at first glance. But once you understand how they work—and why we use them—they become a natural part of math success.
Whether you’re adding, subtracting, multiplying, or dividing, the steps are clear. With practice, your child can master improper fractions and even enjoy the process.
Try out sample problems. Watch the videos. Use The Teacher’s Dungeon for interactive practice.
Let’s turn fraction fear into fraction confidence. ➗
✨ Ready to Learn More?
Sign up for a FREE trial of The Teacher’s Dungeon and explore more game-based lessons with built-in video support. Empower your child to succeed—one fraction at a time!

#ImproperFractions #FractionsMadeEasy #MathConfidence #TheTeachersDungeon #FractionHelp #HomeschoolMath #ParentMathSupport #GamifiedLearning