Welcome to Illustrating Fractions: Unlocking Math Success with Visual Learning
Mastering fractions can feel like solving a puzzle without the picture on the box. But with the right strategies, learning fractions becomes simple, engaging, and even fun! In this guide, you’ll discover proven techniques that help children build a strong foundation in fractions through visual models and interactive video tutorials.
By the end of this article, you’ll understand how to use visual strategies to teach fractions effectively, while giving your child the tools they need to excel in math.
Why Do So Many Students Struggle with Fractions?
Fractions are often challenging because they are abstract concepts. Without clear visual aids, students can struggle to grasp what fractions truly represent.
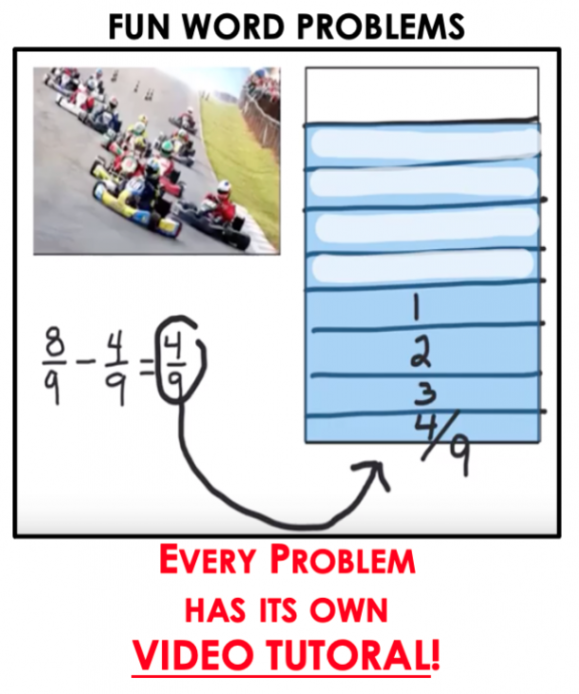
That’s why my step-by-step video tutorials use mathematical models to make learning fractions simple and effective. This visual approach helps students:
✅ Understand fractions as parts of a whole
✅ See why common denominators are essential
✅ Grasp why multiplying fractions makes numbers smaller while dividing makes them larger
Most importantly, these visual strategies build math confidence and help children genuinely enjoy learning fractions.
Mathematical Models
Make Abstract Concepts Concrete!
By drawing Mathematical Models, your child will understand…
- That fractions are simply parts of a whole!
- Why you must have common denominators when adding or subtracting!
- Why an improper fractions is more than a whole, and how to write it as a mixed number!
- How to borrow from a whole number, to make an improper fraction, so you can subtract a smaller fraction from a bigger one!
- Why your answer is smaller when you multiply fractions, and bigger when you divide fractions!
- But Most importantly – you will gain a concrete understanding of fractions, that will help you to excel, and actually enjoy doing the math!
A Proven Strategy That Transforms Learning
The solution lies in turning abstract fraction problems into concrete visual models. In this FREE “How to Do Fractions” video series, your child will learn two powerful strategies that simplify fractions:
- Draw a box ✏️ – Divide it into the number of parts shown by the denominator.
- Color the parts ✨ – Shade the number of parts indicated by the numerator.
These simple yet effective steps create a visual understanding that helps children connect the dots and grasp the logic behind fractions.
Most people have a difficult time understanding fractions, because they never took the time to illustrate what is happening when you are working with fractions.
Mathematical Models are the most effective strategy I have ever found for developing a concrete understanding of fractions. When you draw mathematical models, it makes the abstract concepts of math concrete, and then you can understand fractions at a deeper level. One you understand why something works, you will begin to excel, and actually enjoy doing the math.
Mathematical Models
Make Abstract Concepts Concrete!
Step-by-Step Video Tutorials with Real-World Scenarios
Our engaging video tutorials bring fractions to life using fun, relatable stories that keep kids engaged.
Cyclical Learning Approach
I have incorporated a cyclical learning approach with math tutorial videos. Each educational concept is introduced, then reinforced, then revisited again and again to ensure success. I have broken this series on fractions into 11 different books. In this first Blog Post, I will introduce the first three books, which introduce How to illustrate a fraction, then how to add and subtract fractions with like denominators.
Here is a quick link to each of the three blog Posts:
Mastering Fractions: Understanding the Basics with Engaging Videos Tutorials!
Master Fractions: Multiplying & Dividing Fractions: Unlocking Math Success for Your Child!
I have scaffold these problems:
-
- The first problem is a Watch ME.
Students should read the problem and then click on the video to watch how the problem is solved.
Students should copy the entire problem into their notebook. - The second problem is a WORK WITH ME.
Students should read the problem then gather all their materials, so that they can do the problem with me.
Students should play the math tutorial video and pause it when told.
Finally, Students should copy the problem down on their own paper, and solve it with me.
When the math tutorial video is complete, students should review the problem with their teacher or parent. - All the following problems are ON YOUR OWN.
Students should solve the problems just as they did in the first two.
Once you they completed the problem, they should watch the math tutorial video.
Students should keep their paper with them while they watch the video.
If they made a mistake, they should pause the math tutorial video and fix their mistake.
That’s the fastest way to learn!
- The first problem is a Watch ME.
Book 1
Illustrating Basic Fractions
Challenge 1: “Watch Me”
Brownie Bandit – Puppy in a Seatbelt!
Play WATCH ME
For this first problem, simply watch how the problem is solved. ✨
Relax and focus on the strategies for solving the problem above.
When the video is complete, copy the problem into your notebook
or on a piece of paper for your parent or teacher.
Puppy in a Seatbelt Your child will watch a tutorial where a curious puppy sneaks out of his seatbelt and devours part of a pan of brownies. With only 4/6 of the brownies left, your child will illustrate and solve the problem by drawing a visual model.
Watch the Free Video Tutorial by clicking on the video by clicking on the photo of Brownie Bandit Pup below.
Challenge 2: “Work with Me”
Pizza Stealing Ram!
Once a month, your dad buys a pizza and cuts it into 1/3 parts for the
family. Just as you’re about to eat, a ram bursts in and starts munching!
There is only 2/3 of the pizza left. Can you illustrate how much is
left?
WORK WITH ME
Play the video by clicking on the photo of Pizza Stealing Ram.
Pause the video when told.
Copy the problem down on your own paper, and solve it with me.
Pay close attention! Your next challenge will be very similar to this
one.
Watch the Free Video Tutorial by clicking on the video by clicking on the photo of Pizza Stealing Ram.
Challenge 3: “On Your Own”
Party Crashing Cow!
Your parents buy a beautiful birthday cake and cut it into 1/9 parts. While you
and your friends are playing, a mother cow and her baby sneak up and start
eating!
There is only 5/9 of the cake left. Can you illustrate how much is left?
On Your Own Challenge!
Complete this problems first ✏
Then, Click on Party Crashing Cow to Watch the Free Video Tutorial
Drill & Kill
This is where we Drill until we Kill all our mistakes!
I call this section of the book, Drill & Kill, because we will drill this concept until we are perfect, and we kill any mistakes!
The following problems can all be solved with the same strategies we used to solve the first ten problems.
- Solve all four problems on each page.
- Watch the video & correct your work.
- Review your work with your parent or teacher.
If you get all 4 problems correct, your parent or teacher may tell you that you’re ready to move to the next book/article within this series.
Good Luck!
Drill & Kill
|
Problem 1 Can you illustrate 3/5? |
Problem 2
Can you illustrate 7/9?
|
| Problem 3
Can you illustrate 1/4?
|
Problem 4 Can you illustrate 4/7?
|
Once you complete the problem – Hit PLAY on the math tutorial video below. Good Luck!
Book 2
Adding Fractions with Common Denominators
Mathematical Model
Challenge 1: Watch Me – Math Ninja Celebration
The Math Ninja’s Cake Party!
You just won the “Math Ninja” award at school for solving fraction problems!
To celebrate, your mom makes two cakes: one chocolate and one lemon .
You cut each cake into 1/7 parts but can’t resist eating a few slices!
Now, only 3/7 of the chocolate cake and 4/7 of the lemon cake are left.
How much cake do you have in all?
✅ Watch the FREE video tutorial here:
Challenge 2: Work With Me – Dog-Food Stealing Raccoon
Problem: The Dog-Food Stealing Raccoon!
A sneaky raccoon has been breaking into your garage for two nights,
eating your dog’s food! Each time, he hides behind a tree :
● Night 1: He hides 3/5 of his body.
● Night 2: He hides 4/5 of his body.
How much of his body did the raccoon hide in total?
✅ Watch the FREE video tutorial here:
Challenge 3: On Your Own – Trumpet-Playing Dog
Problem: Rex, the Trumpet-Playing Dog!
Your dog Rex is a trumpet-playing star! But whenever he sees a cat , he
drops everything to chase it!
● Fire Department Performance: He finishes 2/9 of the song before a cat
distracts him.
● Librarians’ Convention: He completes 4/9 of a song before another cat
appears!
How much of his songs did Rex play before chasing cats?
On Your Own Challenge!
Complete this problems first ✏
✅ Then, Click on Rex, the Trumpet-Playing Dog below and Watch the FREE video tutorial:
Drill & Kill
This is where we Drill until we Kill all our mistakes!
Problem 13/5 + 2/5? |
Problem 27/9 + 3/9? |
Problem 33/4 + 3/4? |
Problem 44/7 + 4/7? |
Once you complete the problem – Hit PLAY on the math tutorial video below. Good Luck!
Mathematical Model
️ Challenge 1: National Go-Kart Race (Watch Me)
The race is 8/9 of a mile long.
You’ve driven 4/9 of the course so far.
How much farther must you go to win the race?
Watch this free math tutorial video now and follow along as I guide your child step-by-step:
Challenge 2: Kangaroo Feeding Time (Work With Me)
You feed a kangaroo 2/7 of a bag of food.
The bag originally held 5/7.
How much food is left?
Watch this guided tutorial video to solve the problem together:
Challenge 3: Baby Elephant Bath (On Your Own)
Two playful elephants spend 6/7 of an hour playing in the river.
They’ve already been in for 5/7 of an hour.
How much more time do they have to play?
Watch this free video tutorial to review your answer:
This book includes 10 word problems like the three above plus another 16 Drill & Kill problems like the 4 below. All of my math books are included FREE with your membership to The Teacher’s Dungeon. The Teacher’s Dungeon is a highly effective Math Intervention game that makes learning FUN! Click Here to Check It Out!
Drill & Kill
This is where we Drill until we Kill all our mistakes!
Problem 13/5 – 2/5? |
Problem 27/9 – 3/9? |
Problem 33/4 – 1/4? |
Problem 46/7 – 4/7? |
Once you complete the problem – Hit PLAY on the math tutorial video below. Good Luck!
Unlock Full Access to All Math Books and Resources
The sample problems and video tutorials you see here are just the beginning! All my math books — filled with engaging stories, practice problems, and video tutorials — are available FREE with your membership to The Teacher’s Dungeon.
Join The Teacher’s Dungeon Today and Give Your Child the Math Support They Deserve!
Your membership unlocks: ✅ Access to all math books
✅ Step-by-step video tutorials for each lesson
✅ Engaging stories that make math fun
Don’t let fractions hold your child back. Help them build math confidence today!
Click here to learn more about The Teacher’s Dungeon!
Conclusion: Turn Math Struggles into Math Success
If your child has ever felt frustrated or discouraged by fractions, there’s hope! By using simple visual strategies, engaging video tutorials, and step-by-step guidance, your child can master fractions with confidence and excitement.
Is there any updates coming soon from this site?
Hi Selo –
I am sorry for the delay. At the end of the school year (last year), I was asked to create a series on my method of teaching division. We have a number of students at my school who struggle with long division, and I have created an alternative called area division. I created the series, but it took me all summer to complete it.
Now school is back in session, and I am teaching full time, but I will do my best to complete this series on fraction.
Thanks for reminder that I need to get back to work on fractions.
In the meantime – if you need help with division, check out Area Division
http://teachersdungeon.com/blog/long-division-answers-there-is-an-easier-way/
Have a great day!
Hi Brian, your “11-Steps to FULLY Understand Fractions” is so brilliant. You have a very profound knowledge on fractions. You have presented a lot of ideas on how to deal with fractions. This is very helpful to all kind of students and also to all teachers. Regarding adding and subtracting fractions, let me also share my idea on how to deal with fractions.
Adding and Subtracting fractions maybe difficult at first but keeping on practicing will make it easier in the long run. To add and subtract fractions successfully is to make the rules stick to your memory. So I have to mention again the rules here.
Rules are:
Same denominator:
Add both numerators then reduce. The result would be the final answer.
Different denominator (4 steps):
1. Multiply the numerator of first fraction to the denominator of second fraction. The result is the new numerator of first fraction.
2. Multiply the numerator of the second fraction to the denominator of first fraction. The result is the new numerator of second fraction.
3. Multiply both denominators. The result is the common denominator for two fractions.
4. Add the two new numerators. The result is the answer.
To make it stick to your memory:
Rules for subtraction:
Same denominator:
Subtract second numerator from first then reduce. The result would be the final answer.
Different denominator (4 steps):
1. Multiply the numerator of first fraction to the denominator of second fraction. The result is the new numerator of first fraction.
2. Multiply the numerator of the second fraction to the denominator of first fraction. The result is the new numerator of second fraction.
3. Multiply both denominators. The result is the common denominator for two fractions.
4. Subtract new second numerator from first new numerator. The result is now the answer.
To make it stick to your memory:
Same numerator:
Add two fractions 50 times.
Subtract two fractions 50 times.
Different denominator:
Add two fractions 100 times.
Subtract two fractions 100 times.
To check if your answer is right and your step by step solution is correct:
Use fraction calculator with button from http://www.fractioncalc.com to be sure that your fraction solution is correct.
The key here is to make the rules implanted into the minds of the students so that they will never forget.
Hello Anne –
Thank you for your kind words and great advice.
I really like your suggestion to practice working with fractions until it become easy. I also like your suggestion to solve problems and then check your work with the the fractions calculator website.
Have a fantastic day – Brian